Skip to main content
Version: User Guides (Cloud)

ANN Search Explained

A k-nearest neighbor (kNN) search finds the k-nearest vectors to a query vector. Specifically, it compares a query vector to every vector in a vector space until k exact matches appear. Although kNN searches guarantee perfect accuracy, they are time-consuming, especially for large datasets comprising high-dimensional vectors.

In contrast, approximate nearest neighbor (ANN) searches require building an index beforehand. Various indexing algorithms demonstrate trade-offs among search speed, memory usage, and accuracy. Generally, two paths are available to implement these algorithms: narrowing the search scope and decomposing high-dimensional vector spaces into low-dimensional subspaces.

Narrowing the search scope can reduce search time by selecting only a subset of possible candidates for comparison with the query vector. This avoids irrelevant vectors. To determine whether a vector is in the subset, an index structure is needed to sort the vectors.

There are generally three ideas available for forming the index structure: graphs, trees, and hashes.

HNSW: A graph-based indexing algorithm​

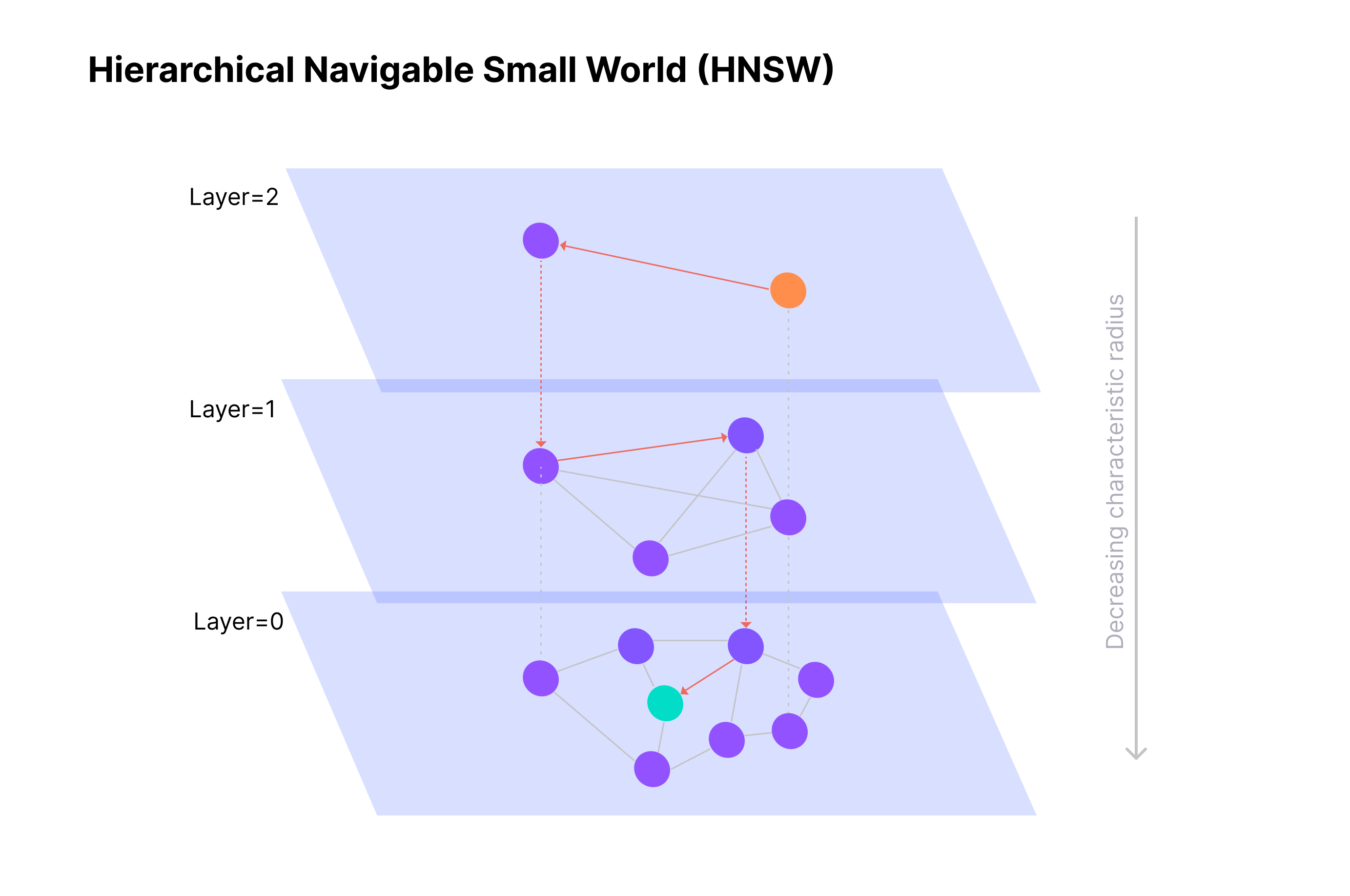
Hierarchical Navigable Small World (HNSW) indexes a vector space by creating a hierarchical proximity graph. Specifically, HNSW draws proximity links (or edges) between vectors (or vertices) on each layer to form a single-layer proximity graph and stacks them up to form the hierarchical graph. The bottom layer holds all vectors and their proximity links. As the layer goes up, only a smaller set of vectors and proximity links remains.

Once the hierarchical proximity graph is created, the search goes as follows:

  1. Find a vector as the entry point on the top layer.

  2. Move gradually to the nearest vector along the available proximity links.

  3. Once you determine the nearest vector at the top layer, use the same vector at a lower layer as the entry point to find its nearest neighbor at that layer.

  4. Repeat the preceding steps until you find the nearest vector at the bottom layer.

hnsw-explained

LSH: A hash-based ANN indexing algorithm​

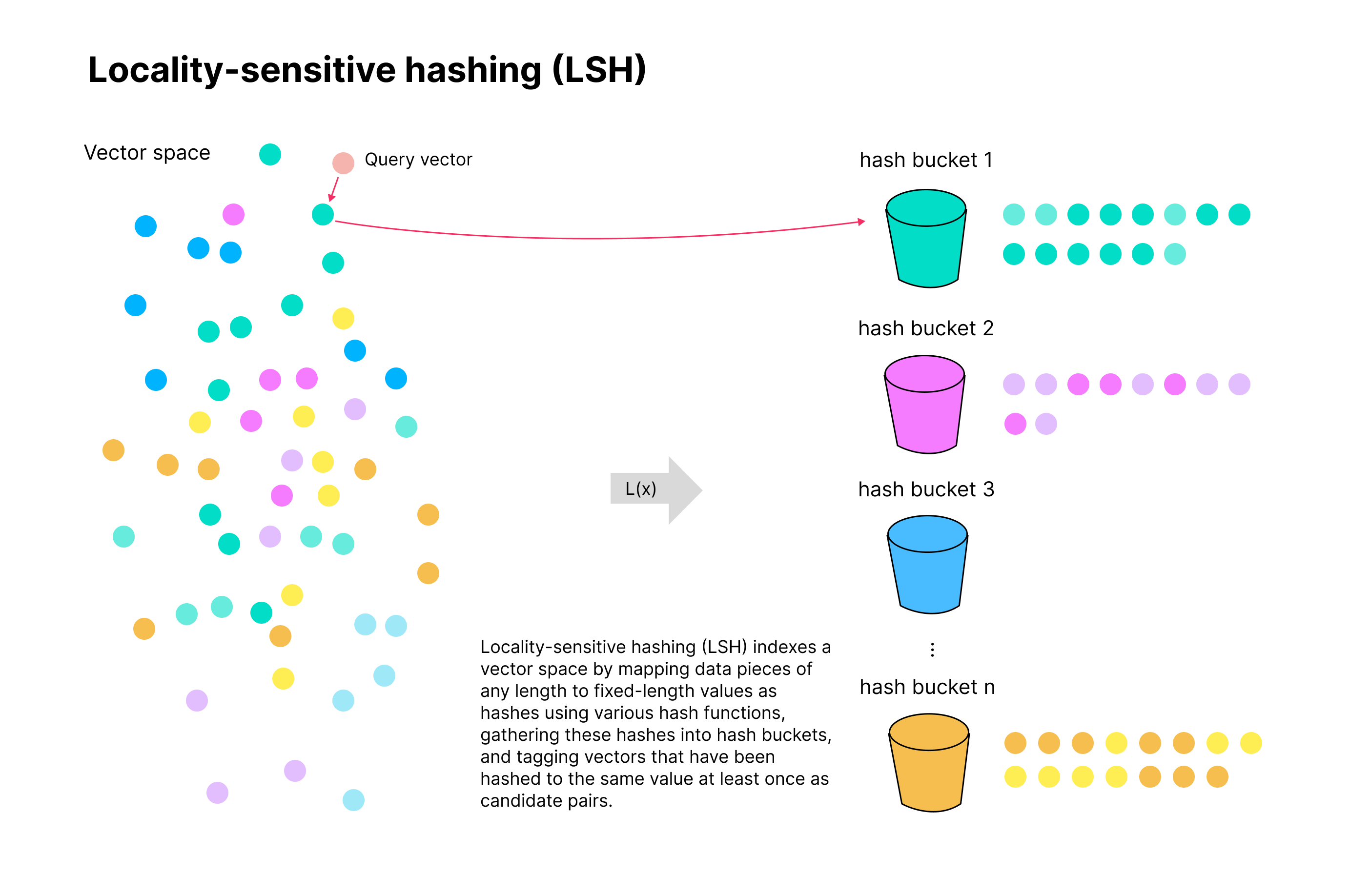
Locality-sensitive hashing (LSH) indexes a vector space by mapping data pieces of any length to fixed-length values as hashes using various hash functions, gathering these hashes into hash buckets, and tagging vectors that have been hashed to the same value at least once as candidate pairs.

locality_sensitive_hashing

DiskANN: ANN search on disk based on Vamana graphs​

Unlike HNSW that builds a hierarchical graph for layered searches, Vamana’s indexing process is relatively simple:

  1. Initialize a random graph;

  2. Find the navigation point by first locating the global centroid and determining the closest point. Use a global comparison to minimize the average search radius.

  3. Perform Approximate Nearest Neighbor Search with the initialized random neighbor graph and search starting point from step 2. Use all points on the search path as candidate neighbor sets and apply the edge trimming strategy with alpha = 1 to reduce the search radius.

  4. Repeat step 3 with adjusted alpha > 1 (1.2 recommended in the paper) to improve graph quality and recall rate.

Once the index is ready, the search goes as follows:

  1. Load relevant data, including query set, PQ center point data, codebook data, search starting point, and index meta.

  2. Use the indexed data set to perform cached_beam_search, count the access times of each point, and cache the num_nodes_to_cache points with the highest access frequency.

  3. WARMUP operation is performed by default using the sample data set to perform a cached_beam_search.

  4. Perform cached_beam_search with the query set for each given parameter L, and output statistics such as recall rate and QPS. Warmup and hotspot data statistics are not included in query time.

For details, refer to DiskANN, A Disk-based ANNS Solution with High Recall and High QPS on Billion-scale Dataset.